[이코테] 6. 정렬 알고리즘 - 선택, 삽입, 퀵, 계수정렬 — 테크 조랭이떡

정렬 알고리즘

정렬(Sorting)이란 데이터를 특정한 기준에 따라 순서대로 나열하는 것을 말함.
일반적으로 문제 상황에 따라서 적절한 정렬 알고리즘이 공식처럼 사용됨.
선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬 등이 있음.

선택 정렬

핵심 동작 원리
- 처리되지 않은 데이터 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복함.
선택 정렬의 시간 복잡도
- 선택 정렬은 N번 만큼 가장 작은 수를 찾아서 맨 앞으로 보내야 함.
- 구현 방식에 따라서 사소한 오차는 있을 수 있지만, 전체 연산 횟수는 다음과 같음
  - N + (N -1) + (N-2) + ... + 2
- 이는 (N^2 + N - 2) / 2 로 표현할 수 있는데, 빅오 표기법에 따라서 O(N^2)이라고 작성.

예시

데이터

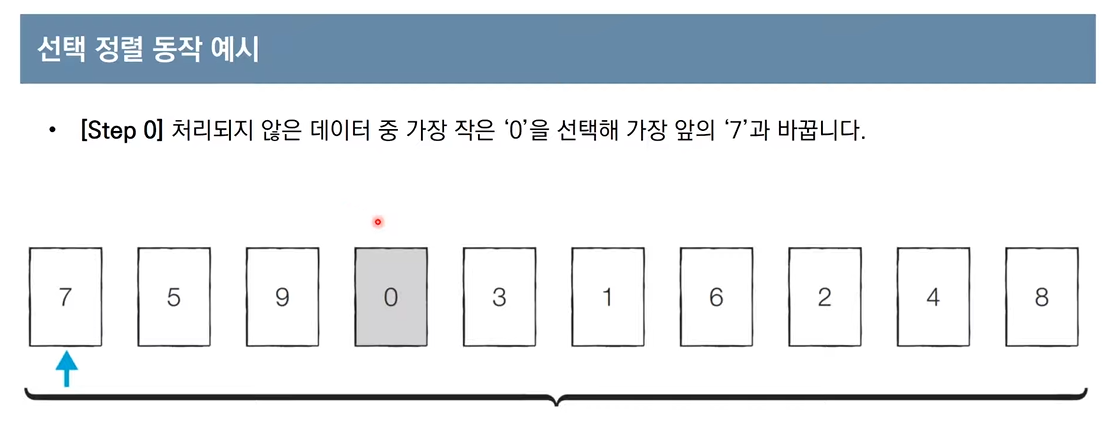
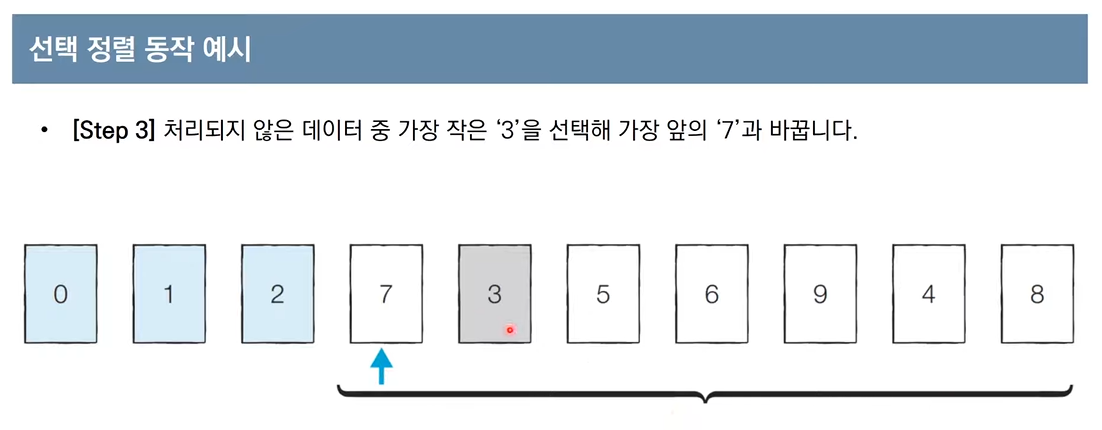
이런 방식으로 선택 정렬을 이해하면 되고,

2중 반복문으로 구현해낼 수 있다.

선택 정렬 소스코드

array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(len(array)):
    min_index = i # 가장 작은 원소의 인덱스
    for j in range(i + 1, len(array)):
        if array[min_index] > array[j]:
            min_index = j
    array[i], array[min_index] = array[min_index], array[i] # 스와프

print(array)

'''output
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
'''

삽입 정렬

핵심 동작 원리
- 처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입합니다.
- 선택 정렬에 비해 구현 난이도가 높은 편이지만, 일반적으로 더 효율적으로 동작합니다.
삽입 정렬의 시간 복잡도
- 삽입 정렬의 시간 복잡도는 O(N^2)이며, 선택 정렬과 마찬가지로 반복문이 두 번 중첩되어 사용됨.
- 삽입 정렬은 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 작동합니다.
  - 최선의 경우 O(N)의 시간 복잡도를 가짐.
  - 이미 정렬되어 있는 상태에서 다시 삽입 정렬을 수행하면 어떻게 될까? 답 : O(N)
    - 각 원소가 들어갈 위치를 찾는데에 선형 탐색을 하게됨.(단순히 상수시간으로 대체됨)

예시

데이터

삽입 정렬 소스 코드

array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(1, len(array)):
    for j in range(i, 0, -1): # 인덱스 i부터 1까지 1씩 감소하며 반복하는 문법
        if array[j] < array[j-1]: # 한 칸씩 왼쪽으로 이동
            array[j], array[j-1] = array[j-1], array[j] # 스와핑
        else: # 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
            break

print(array)

'''output
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
'''

퀵 정렬

기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법임.
일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나
병합 정렬과 더불어 대부분의 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘임.
가장 기본적인 퀵 정렬은 첫 번째 데이터를 기준 데이터(Pivot)로 설정함.
퀵 정렬이 빠른 이유(직관적으로 이해해보자.)
- 이상적인 경우 분할이 절반씩 일어난다면 전체 연산 횟수로 O(NlogN) 가능.
  - 너비 X 높이 = N x logN = NlogN

퀵 정렬의 시간 복잡도
- 퀵 정렬은 평균의 경우 O(NlogN)
- 하지만 최악의 경우 O(N^2)
  - 첫 번째 원소를 피벗으로 삼을 때, 이미 정렬된 배열에 대해서 퀵 정렬 수행시 어떻게 될까?
    1. 0을 피벗으로 설정
    2. 0보다 큰 데이터를 왼쪽에서부터 찾음 (=1)
    3. 0보다 작은 데이터를 오른쪽에서 부터 찾음 (=없음, 0이 골라짐)
    4. 자기자신을 고르기 때문에 왼쪽 분할에는 값이 없고, 오른쪽 분할만 존재함.
    5. 그리고 다시, 1을 피벗으로 설정해서 [1. ~ 3.] 반복.
      - 이런 과정이 최악의 경우이며 O(N^2)의 시간 복잡도를 가지게 됨. (유의)
      - 다양한 프로그래밍 언어에서 표준 정렬 라이브러리를 제공할 때, 퀵 정렬을 기반으로 라이브러리가 작성되어 있다면 최악의 경우에도 O(NlogN)을 보장할 수 있도록 구현함.
      - 그래서, 우리가 첫 번째 값을 피벗으로 설정하는 퀵 정렬을 직접 작성한다고 하면 O(N^2)이 나올 수 있다는 것, 그리고 표준 정렬 라이브러리를 사용한다면 O(NlogN)이 보장된다는 것을 기억해야함.

예시

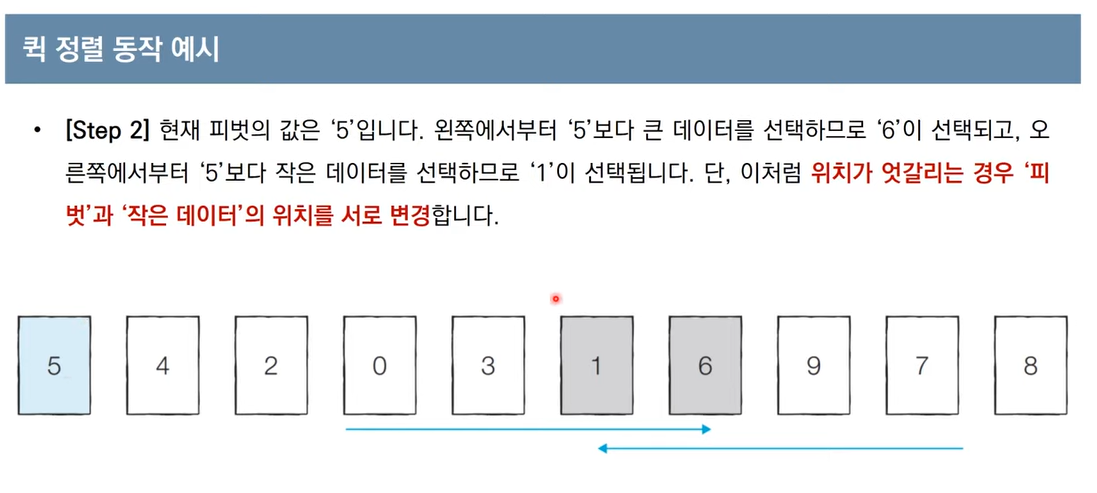
왼쪽은 피벗 값 보다 작은 값들의 모음.

오른쪽은 피벗 값 보다 큰 값들의 모음.

이렇게 '분할(Divide)' 된다.

여기서 왼쪽, 오른쪽 각각 다시 퀵 정렬을 수행한다.

이러한 과정을 재귀적으로 하면 된다.

퀵 정렬 소스 코드

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array, start, end):
    if start >= end: # 원소가 1개인 경우 종료
        return
    pivot = start # 피벗은 첫 번째 원소
    left = start + 1
    right = end
    while(left <= right):
        # 피벗보다 큰 데이터를 찾을 때 까지 반복
        while(left <= end and array[left] <= array[pivot]):
            left += 1
        # 피벗보다 작은 데이터를 찾을 때 까지 반복
        while(right > start and array[right] >= array[pivot]):
            right -= 1
        if(left > right): # 엇갈렸다면 작은 데이터와 피벗을 교체
            array[right], array[pivot] = array[pivot], array[right]
        else:
            array[left], array[right] = array[right], array[left]
    # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
    quick_sort(array, start, right-1)
    quick_sort(array, right + 1, end)

quick_sort(array, 0, len(array)-1)
print(array)

'''output
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
'''

퀵 정렬 소스 코드 : 파이썬의 장점을 살린 방식

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array):
    # 리스트가 하나 이하의 원소만을 담고 있다면 종료
    if len(array) <= 1:
        return array
    pivot = array[0] # 피벗은 첫 번째 원소
    tail = array[1:] # 피벗을 제외한 리스트
    
    left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
    right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
    
    return quick_sort(left_side) +[pivot] + quick_sort(right_side)

print(quick_sort(array))

'''output
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
'''

계수 정렬

특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠르게 동작하는 정렬 알고리즘임.
- 계수 정렬은 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용 가능함.
데이터의 개수가 N, 데이터(양수) 중 최댓값이 K일 때 최악의 경우에도 수행 시간 O(N+K)를 보장함.
계수 정렬의 복잡도 분석
- 계수 정렬의 시간 복잡도와 공간 복잡도는 모두 O(N+K)임.
- 계수 정렬은 때에 따라서 심각한 비효율성을 초래할 수 있음.
  - 데이터가 0과 999,999로 단 2개만 존재하는 경우...
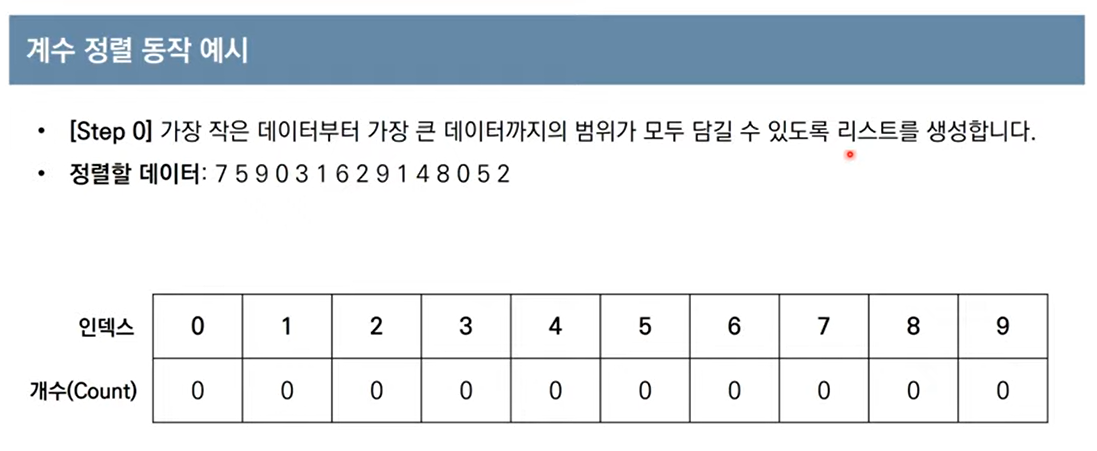
- 계수 정렬은 동일한 값을 가지는 데이터가 여러 개 등장할 때 효과적으로 사용할 수 있음
  - 성적의 경우 100점을 맞은 학생이 여러 명일 수 있기 때문에 계수 정렬이 효과적임.

예시

...

계수 정렬 소스코드

# 모든 원소의 값이 0보다 크거나 같다고 가정
array =[7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
for i in range(len(array)):
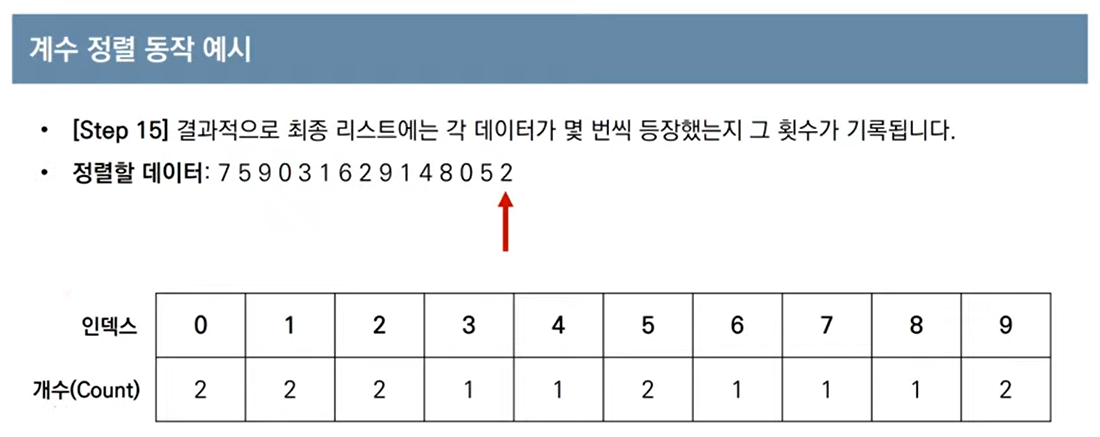
    count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가
3
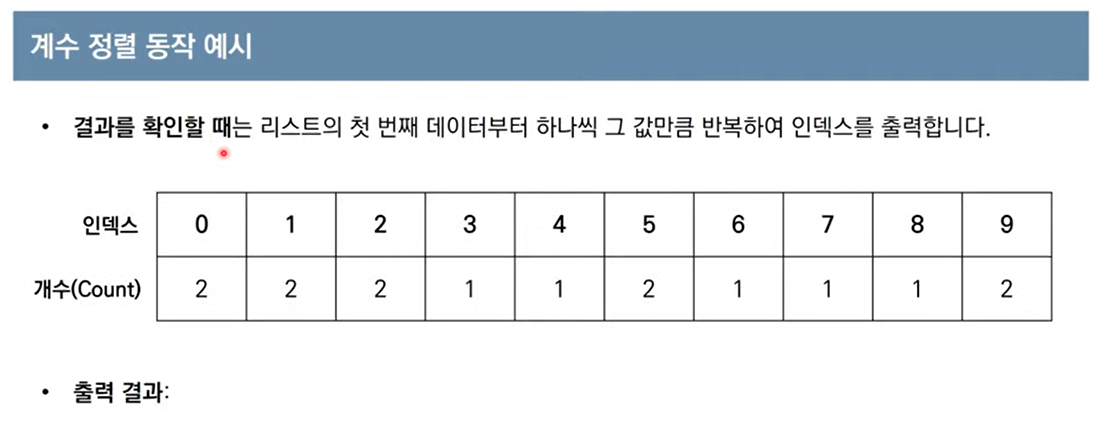
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
    for j in range(count[i]):
        print(i, end=' ') # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력
        
'''output
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9
'''

정렬 알고리즘 비교하기

대부분의 프로그래밍 언어에서 지원하는 표준 정렬 라이브러리는 최악의 경우에도 O(NlogN)을 보장하도록 설계되어 있음.
- 별도로 문제에서 정렬 함수를 구현하라고 명시되어있지 않다면, 일반적으로 표준 정렬 라이브러리를 사용하는 것을 추천함.

이유

정렬 알고리즘	평균 시간 복잡도	공간 복잡도	특징
선택 정렬	O(N^2)	O(N)	아이디어가 매우 간단
삽입 정렬	O(N^2)	O(N)	데이터가 거의 정렬되어 있을 때는 가장 빠름
퀵 정렬	O(NlogN)	O(N)	대부분의 경우에 가장 적합하며, 충분히 빠름
계수 정렬	O(N+K)	O(N+K)	데이터의 크기가 한정되어 있는 경우에만 사용이 가능하지만, 매우 빠르게 동작함.

이코테 2021 시리즈 씹어먹기 by 조랭이떡

시리즈 목차

코딩테스트 출제 경향 및 알고리즘 성능 평가
파이썬 문법 부수기
그리디
구현
DFS & BFS (추후링크)
정렬 알고리즘 (추후링크)
이진 탐색 (추후링크)
다이나믹 프로그래밍 (추후링크)
최단 경로 알고리즘 (추후링크)
기타 그래프 이론 (추후링크)
코딩 테스트에서 자주 출제되는 기타 알고리즘 (추후링크)
개발형 코딩 테스트 (추후링크)

티스토리툴바